What Is Matrix Multiplication Used For

What does matrix multiplication mean? Here'southward a few common intuitions:

1) Matrix multiplication scales/rotates/skews a geometric plane.

matrix intuition

This is useful when start learning about vectors: vectors go in, new ones come out. Unfortunately, this can lead to an over-reliance on geometric visualization.

If 20 families are coming to your BBQ, how practise you gauge the hotdogs you need? (Hrm… xx families, telephone call information technology three people per family, 2 hotdogs each… about 20 * 3 * two = 120 hotdogs.)

Yous probably don't recollect "Oh, I need the volume of a invitation-familysize-hunger prism!". With big matrices I don't think near 500-dimensional vectors, just information to exist modified.

ii) Matrix multiplication composes linear operations.

This is the technically accurate definition: yeah, matrix multiplication results in a new matrix that composes the original functions. Notwithstanding, sometimes the matrix existence operated on is not a linear operation, but a ready of vectors or data points. We need some other intuition for what's happening.

I'll put a developer's viewpoint into the band:

3) Matrix multiplication is about information menstruum, converting information to code and back.

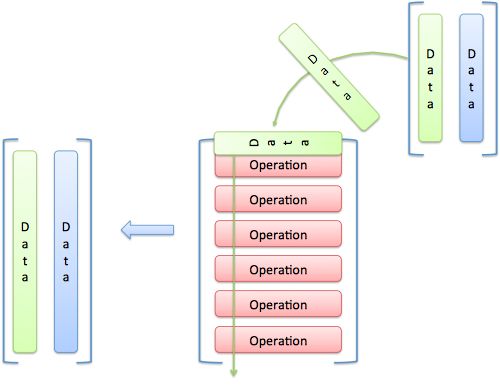
matrix pour

I think of linear algebra as "math spreadsheets" (if you're new to linear algebra, read this intro):

We store information in various spreadsheets ("matrices")
Some of the data are seen as functions to apply, others as information points to employ
We tin can swap betwixt the vector and function interpretation as needed

Sometimes I'll think of data as geometric vectors, and sometimes I'll encounter a matrix equally a composing functions. But more often than not I think about information flowing through a organization. (Some purists cringe at reducing beautiful algebraic structures into frumpy spreadsheets; I slumber OK at night.)

Programmer's Intuition: Code is Data is Code

Have your favorite recipe. If you interpret the words as instructions, you'll end up with a pie, muffin, cake, etc.

If you interpret the words equally data, the text is prose that can be tweaked:

Convert measurements to metric units
Swap ingredients due to allergies
Adjust for distance or different equipment

The result is a new recipe, which tin can be further tweaked, or executed as instructions to make a different pie, muffin, cake, etc. (Compilers treat a program as text, modify it, and somewhen output "instructions" — which could be text for another layer.)

That'southward Linear Algebra. We take raw information like "three 4 v" treat it as a vector or function, depending on how it'south written:

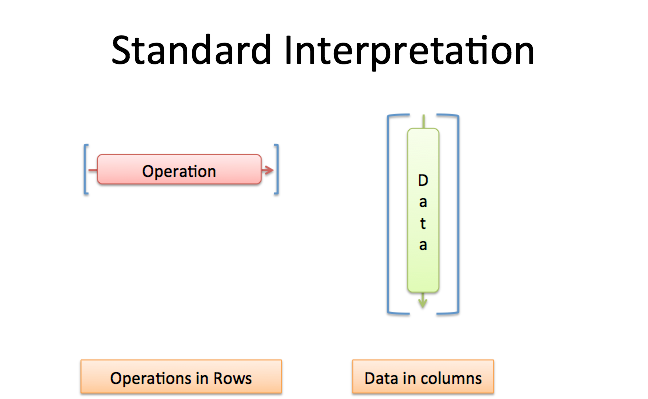
operation and data

By convention, a vertical column is usually a vector, and a horizontal row is typically a function:

[3; 4; five] means 10 = (3, 4, five). Hither, 10 is a vector of data (I'm using ; to separate each row).
[3 4 five] ways f(a, b, c) = 3a + 4b + 5c. This is a function taking iii inputs and returning a unmarried issue.

And the aha! moment: data is code, lawmaking is data!

code and data are equivalent

The row containing a horizontal role could really be three information points (each with a single chemical element). The vertical column of data could really be three distinct functions, each taking a single parameter.

Ah. This is getting neat: depending on the desired outcome, nosotros tin can combine information and code in a different order.

The Matrix Transpose

The matrix transpose swaps rows and columns. Here'south what information technology means in practise.

If ten was a column vector with iii entries ([three; 4; 5]), and so x' is:

A function taking 3 arguments ([3 4 five])
x' can still remain a data vector, merely as three separate entries. The transpose "split it upwardly".

Similarly, if f = [3 4 5] is our row vector, then f' tin can mean:

A single information vector, in a vertical column.
f' is separated into three functions (each taking a single input).

Let's use this in practice.

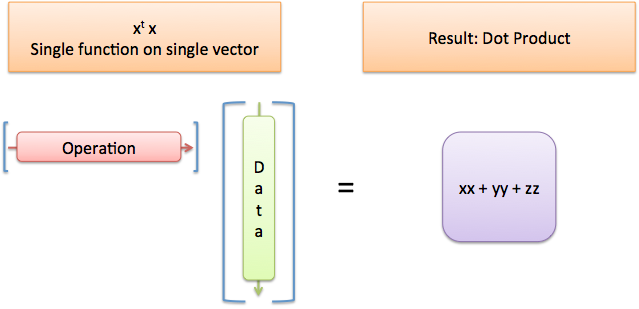
When nosotros encounter 10' * ten we mean: x' (as a single part) is working on x (a single vector). The result is the dot production (read more than). In other words, we've applied the data to itself.

x transform linear algebra

When nosotros meet 10 * 10' we hateful x (as a set of functions) is working on x' (a ready of private data points). The result is a grid where we've practical each function to each data point. Here, nosotros've mixed the information with itself in every possible permutation.

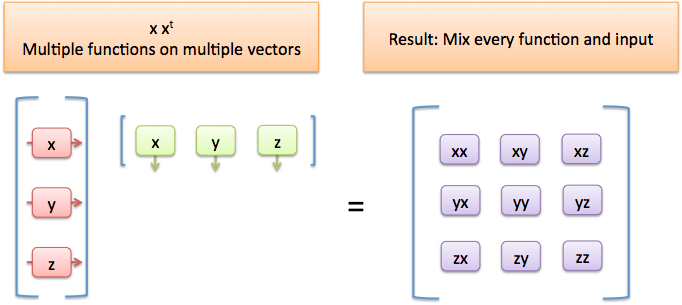
x transpose linear algebra

I recollect of xx as x(10). Information technology's the "function x" working on the "vector ten". (This helps compute the covariance matrix, a measure of cocky-similarity in the information.)

Putting The Intuition To Use

Phew! How does this help us? When we encounter an equation like this (from the Automobile Learning class):

$\displaystyle{\[h_{\theta}(x)=\theta^Tx\] }$

I at present have an instant feel of what'southward happening. In the first equation, we're treating $\theta$ (which is normally a set of data parameters) as a function, and passing in $ten$ as an argument. This should give us a single value.

More complex derivations like this:

$\displaystyle{\[\theta=(X^TX)^{-1}X^Ty\]}$

can be worked through. In some cases it gets catchy considering we store the data as rows (not columns) in the matrix, but now I take much better tools to follow along. Yous tin can outset estimating when you'll go a single value, or when you'll go a "permutation grid" as a consequence.

Geometric scaling and linear composition accept their place, merely here I want to remember about information. "The data in x is becoming a function, and we're passing itself as the parameter."

Long story brusque, don't get locked into a single intuition. Multiplication evolved from repeated addition, to scaling (decimals), to rotations (imaginary numbers), to "applying" ane number to another (integrals), then on. Why not the same for matrix multiplication?

Happy math.

Appendix: What about the other combinations?

Yous may be curious why we tin't utilize the other combinations, similar ten x or 10' ten'. Simply put, the parameters don't line upwardly: nosotros'd have functions expecting 3 inputs only being passed a single parameter, or functions expecting single inputs getting passed three.

Appendix: Javascript Interpretation

The dot product x' * 10 could be seen as the following javascript command:

((x, y, z) => x*3 + y*4 + z*five)(iii, 4, five)

We define an anonymous role of iii arguments, and immediately pass it 3 parameters. This returns 50 (the dot production: 3*three + iv*4 + v*5 = 50).

The math notation is super-meaty, so we tin can simply write (in Octave/Matlab):

octave:2> [3 4 5] * [three 4 5]' ans = 50

Remember that [3 4 5] is the role and [iii; 4; 5] or [3 4 5]' is how we'd write the information vector.

Appendix: Adept Method

This article came about from a TODO in my machine learning course notes that use the ADEPT Method:

I wanted to explain to myself — in plain English — why we wanted 10' x and not the reverse. Now, in patently English: We're treating the information as a office, and passing the aforementioned info as the parameter.